In this post, I will explain the internal mechanisms that allow LSTM networks to perform better when model temporal sequences and their long-range dependencies than the coventional RNNs, We will then use it in real life problem by training LSTM as a multi-class classifier to predict the tag of a programming question on Stack Overflow using Tensorflow/Keras.
Note: In order to understand this post, you must have basic knowledge of recurrent neural networks and Keras. You can refer to recurrent neural network to understand these concepts:
Modeling sequential data using conventional recurrent neural network, sometimes encounter sequences in which the gap between the relevant information and the point where it’s needed is very large, with these kind of huge gaps, RNNs are unable connect information to where it’s needed. During the backpropagation phase of RNNs, in which error signals (gradients) are backpropagated through time, the recurrent hidden layers (weight matrix associated with the layers) are subject to repeated multiplications. These multiplications are determined by the number of timesteps (length of the sequence), and this might result in numerical instability for lengthy sequence. For lengthy sequence, small weights tend to lead to a situation known as vanishing gradients where error signals propagating backwards get so small that learning either becomes very slow or stops working altogether (error signals fowing backwards in time tend to vanish). Conversely larger weights tend to lead to a situation where error signals are so large that they can cause learning to diverge, a situation known as exploding gradients.
To read more on exploding and vanishing gradients have a look at this papers
Understanding the exploding gradient problem
Learning long-term dependencies with gradient descent is difficult
THE VANISHING GRADIENT PROBLEM DURING LEARNING RECURRENT NEURAL NETS AND PROBLEM SOLUTIONS
The vanishing and exploding gradients problem associated with conventional RNNs , limit their abilities when modeling sequences with long range contextual dependencies and to address these issues, more complex RNNs architectures known as Gated Neural Networks (GNNs) have been designed to mitigate these problems by introducing “Gating Mechanism” to control the flow of information in and out of the units that comprise the network layers. There are several GNNs but in this tutorial we will learn about a notable example known Long short-term memory (LSTM) networks (Hochreiter and Schmidhuber, 1997)
Long Short-Term Memory NETWORKS (LSTMs)
LSTM are design to remember information for long periods of time and this is acheived through the use of a memory cell state denoted by \(C_{t}\) which is controled by the gating mechanism. At each time step, the controllable gating mechanisms decide which parts of the inputs will be written to the memory cell state, and which parts of memory cell state will be overwritten (forgotten), regulating information flowing in and out of the memory cell state and this make LSTMs divide the context management problem into two sub-problems: removing information no longer needed from the context and adding information likely to be needed for later decision making to the context. Figure 1 is a A schematic diagram of LSTMs.
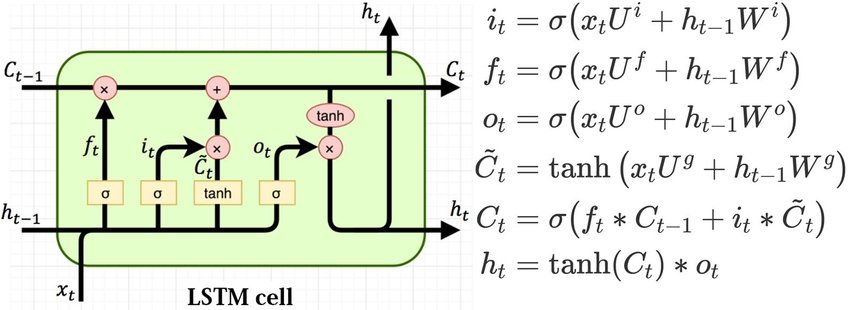 Figure 1
source
Figure 1
source
From Figure 1, the first step of the LSTM model is to decide how to to reset the content of the memory cell and this is controlled by the forget gate denoted as \(f_t\) and defined as
\[f_{t}=\sigma(x_{t}U^{f} +h_{t-1}W^{f} )\]where \(W^{f}\) denotes the hidden to hidden weights with the superscript \(f\) as a symbol indicating the forget gate, \(U^{f}\) denoting input to hidden weights. The forget gate computes the weighted sum of the previous hidden state \(h_{t−1}\) and the current input \(x_{t}\) of time step t (time steps correspond to word positions in a sentence) then passes it through a sigmoid activation function which output a vector with values between 0 and 1. The forgate gate is then multiplied by the previous memory cell \(C_{t-1}\) to decide how much of the previous memory cell content to retain when computing the current memory cell state \(C_{t}\). With a forgate gate value of 0, content of the previous memory cell will be completely discarded and with a value of 1, content of the previous memory cell will be used when computing the current memory cell. Let defined this multiplcation as
\[k_{t}=C_{t-1} \odot f_{t}\]NOTE \(\odot\) the Hadamard product (also known as the element-wise product)
The next step is to compute the actual information (create a contextual vector or Candidate Memory Cell \(C^{t}\) needed to extract from the previous hidden state and current inputs and is defined by
\[\tilde{C_{t}} = tanh(U^{g}x_{t} + W^{g}h_{t−1} )\]NB: This is a contextual vector \(\tilde{C_{t}}\) containing all possible values that needs to be added to the cell state.
The model then decide how information stored in the Candidate Memory Cell is selected and this is regulated by the add or input gate. The input gate is defined as
\[i_{t} = \sigma(U^{i}x_{t} +W^{i}h_{t−1})\]The input gate then select information needed to be added to the current memory cell state via Candidate Memory Cell and is defined as
\[j_{t} = \tilde{C_{t}}\odot i_{t}\]we now defined the current memory cell state \(C_{t}\) as
\[C_{t}=k_{t}+j_{t}=C_{t-1} \odot f_{t} + \tilde{C_{t}}\odot i_{t}\]NB : This is the Cell state that stores information and is responsible for remembering information for long period of time
Not all information stored in the current memory cell state is required for the current hidden state, so the output gate then decides information required for the current hidden state and is defined as
\[o_{t} = \sigma(U^{o}x_{t} +W^{o}h_{t−1})\]The current hidden state $h_{t}$ is then defined as
\[h_{t}=o_{t} \odot tanh(C_{t})\]Let now implement the model using keras
import tensorflow as tf
from tensorflow import keras as K
from tensorflow.keras.layers.experimental.preprocessing import TextVectorization
Loading data
batch_size=124
seed = 100
train_data=K.preprocessing.text_dataset_from_directory(directory='./data/stackoverflow/train',
subset='training',batch_size=batch_size,
seed=seed,
validation_split=0.25)
val_data=K.preprocessing.text_dataset_from_directory(directory='./data/stackoverflow/train',
subset='validation',seed=seed,
validation_split=0.25)
test_data=K.preprocessing.text_dataset_from_directory(directory='./data/stackoverflow/test',
batch_size=batch_size )
Found 8000 files belonging to 4 classes.
Using 6000 files for training.
Found 8000 files belonging to 4 classes.
Using 2000 files for validation.
Found 8000 files belonging to 4 classes.
From the above result, there are 8000 examples of which 75% representing 6000 is used as the training set and 25% (2000) as a validation set. The data has a label categorize into 4 classes
for i,label in enumerate(train_data.class_names):
print('index' ,i,"corresponds to ", label)
index 0 corresponds to csharp
index 1 corresponds to java
index 2 corresponds to javascript
index 3 corresponds to python
for x,y in train_data.take(1):
for i in range(1):
print(x.numpy()[i])
print('\n',y.numpy()[i],'--',train_data.class_names[i],)
break
b'"blank boolean expression for a string in do-while loop public class studentgrades {.. string studentid;. integer numericgrade;.. scanner input = new scanner(system.in);..public void loadstudentgrades(){. do{. system.out.println(""please enter a student id, or enter \'end\' to exit: "");. studentid = input.next();. system.out.println(""please enter numeric grade for the id above: "");. numericgrade = input.nextint();. map.put(studentid, numericgrade);. }. while (studentid !string.equals(""end"")); //this is throwing an error. how is it possible to get this to work?. }.}...i\'m working on this class and am finding it difficult to get the while part of my do-while loop to work the way i was expecting it to. i want to say while studentid is not equal to ""end"" to go through the loop."\n'
1 -- csharp
train_data=train_data.cache().prefetch(tf.data.AUTOTUNE)
val_data=val_data.cache().prefetch(tf.data.AUTOTUNE)
test_data=test_data.cache().prefetch(tf.data.AUTOTUNE)
def process_data(data):
lower_data=tf.strings.lower(data)
lower_data=tf.strings.strip(lower_data)
return tf.strings.regex_replace(lower_data,"<b />",' ')
sequence_length = 100
vocab_size = 1000
encoder=TextVectorization(max_tokens=vocab_size, output_mode='int',standardize=process_data,
output_sequence_length=sequence_length)
encoder.adapt(train_data.map(lambda x,y:x))
class LSTM(K.models.Model):
def __init__(self,input_encoder):
super(LSTM,self).__init__()
self.input_encoder=input_encoder
self.embed=K.layers.Embedding(input_dim=vocab_size,input_length=sequence_length,
output_dim=16)
self.lstm_layer=K.layers.LSTM(32,recurrent_dropout=.2)
self.flat=K.layers.Flatten()
self.dropout=K.layers.Dropout(0.3)
self.dense=K.layers.Dense(4,activation='softmax')
def call(self,x):
x=self.input_encoder(x)
x=self.embed(x)
h=self.lstm_layer(x)
h=self.dropout(self.flat(h))
output=self.dense(h)
return output
lstm_model=LSTM(input_encoder=encoder)
lstm_model.compile( optimizer='rmsprop', loss='sparse_categorical_crossentropy',metrics=['acc'])
lstm_model.fit(train_data,batch_size=batch_size,validation_data=val_data,epochs=20)
Epoch 1/20
49/49 [==============================] - 16s 231ms/step - loss: 1.3839 - acc: 0.2566 - val_loss: 1.3815 - val_acc: 0.2735
Epoch 2/20
49/49 [==============================] - 8s 162ms/step - loss: 1.3604 - acc: 0.3101 - val_loss: 1.2764 - val_acc: 0.4270
Epoch 3/20
49/49 [==============================] - 8s 157ms/step - loss: 1.2614 - acc: 0.4029 - val_loss: 1.1663 - val_acc: 0.4500
Epoch 4/20
49/49 [==============================] - 9s 182ms/step - loss: 1.1564 - acc: 0.4484 - val_loss: 1.1934 - val_acc: 0.4285
Epoch 5/20
49/49 [==============================] - 8s 155ms/step - loss: 1.1034 - acc: 0.4842 - val_loss: 1.0685 - val_acc: 0.4845
Epoch 6/20
49/49 [==============================] - 8s 161ms/step - loss: 1.0649 - acc: 0.4994 - val_loss: 1.0873 - val_acc: 0.4920
Epoch 7/20
49/49 [==============================] - 8s 163ms/step - loss: 1.0293 - acc: 0.5187 - val_loss: 1.0622 - val_acc: 0.5055
Epoch 8/20
49/49 [==============================] - 8s 169ms/step - loss: 1.0013 - acc: 0.5511 - val_loss: 1.0052 - val_acc: 0.5310
Epoch 9/20
49/49 [==============================] - 8s 160ms/step - loss: 0.9938 - acc: 0.5615 - val_loss: 1.0364 - val_acc: 0.5315
Epoch 10/20
49/49 [==============================] - 8s 157ms/step - loss: 0.9676 - acc: 0.5777 - val_loss: 1.0216 - val_acc: 0.5515
Epoch 11/20
49/49 [==============================] - 8s 159ms/step - loss: 0.9291 - acc: 0.5861 - val_loss: 1.0288 - val_acc: 0.5535
Epoch 12/20
49/49 [==============================] - 8s 159ms/step - loss: 0.8900 - acc: 0.6114 - val_loss: 1.0212 - val_acc: 0.5575
Epoch 13/20
49/49 [==============================] - 8s 163ms/step - loss: 0.8357 - acc: 0.6408 - val_loss: 1.1499 - val_acc: 0.5635
Epoch 14/20
49/49 [==============================] - 8s 159ms/step - loss: 0.8424 - acc: 0.6491 - val_loss: 1.0042 - val_acc: 0.5900
Epoch 15/20
49/49 [==============================] - 9s 174ms/step - loss: 0.7966 - acc: 0.6664 - val_loss: 0.8653 - val_acc: 0.6285
Epoch 16/20
49/49 [==============================] - 9s 176ms/step - loss: 0.7437 - acc: 0.6879 - val_loss: 0.9403 - val_acc: 0.6265
Epoch 17/20
49/49 [==============================] - 8s 171ms/step - loss: 0.7550 - acc: 0.6924 - val_loss: 0.9791 - val_acc: 0.6265
Epoch 18/20
49/49 [==============================] - 9s 183ms/step - loss: 0.7420 - acc: 0.7027 - val_loss: 0.9143 - val_acc: 0.6355
Epoch 19/20
49/49 [==============================] - 9s 176ms/step - loss: 0.7129 - acc: 0.7033 - val_loss: 0.9438 - val_acc: 0.6395
Epoch 20/20
49/49 [==============================] - 9s 185ms/step - loss: 0.7122 - acc: 0.7035 - val_loss: 1.0339 - val_acc: 0.6300
<tensorflow.python.keras.callbacks.History at 0x2cfc07b22e8>
let evaluate our model on the test set
lstm_model.evaluate(test_data)
65/65 [==============================] - 13s 172ms/step - loss: 1.0457 - acc: 0.6405
[1.0457446575164795, 0.640500009059906]
Let use the model to predict the sample below from the test set.
according the text data the label for the samples are as follows:
| sample | Label |
|---|---|
| sample 1 | python |
| sample 2 | javascript |
| sample 3 | java |
| sample 4 | python |
sample=["variables keep changing back to their original value inside a while loop i am doing the mitx 6.00.01x course and i am on the second problem set on the 3rd problem and i am stuck. .my code: .. balance = 320000. annualinterestrate = 0.2. monthlyinterestrate = (annualinterestrate) / 12.0. monthlyfixedpayment = 0. empbalance = balance. lowerbound = round((balance)/12,2). upperbound = (balance*(1+monthlyinterestrate)**12)/12. monthlyfixedpayment = round( ( (lowerbound+upperbound)/2) ,2). while tempbalance != 0: . monthlyfixedpayment = round( ( (lowerbound+upperbound)/2) ,2) . for m in range(12) :. tempbalance -= monthlyfixedpayment . tempbalance += (monthlyinterestrate)*(tempbalance). tempbalance = round(tempbalance,2) . if tempbalance > 0:. lowerbound = round(monthlyfixedpayment,2). tempbalance = balance. elif tempbalance < 0: . upperbound = round(monthlyfixedpayment,2). tempbalance = balance.. print('lowest payment: ' + str(round(monthlyfixedpayment,2)))...my code uses bisection search to generate the monthlyfixedpayment but after i get to the lines at the end that changes the upperbound or lowerbound values and then start the loop again, the lowerbound and upperbound values reset to their values to the ones outside the loop. does anyone knows how to prevent this?",
"how pass window handler from one page to another? (blank) i have a very strange problem , please don’t ask me why do i need this….i have a page1. page1 has a link which opens new window (page2) using window.open function..chatwindow is a handler of child window with returns from window.open function..now i'm moving from page1 to page3 (by link <a href=""...."" target=""_self"">some text</a>). and i need to check on the page3 if page2 is close or open..how to pass handler chatwindow from page1 to page3?..thank you in advance!",
"what is the difference between text and string? in going through the blankfx tutorial i've run into the text, and it's being used where i would have thought a string would be used. is the only difference between..string foo = new string(""bat"");...and..text bar = new text(""bat"");...that bar cannot be edited, or are there other differences that i haven't been able to find in my research?",
"idiomatic blank iterating and adding to a dict i'm running through a string, creating all substrings of size 10, and adding them to a dict. this is my code,..sequence_map = {}.for i in range(len(s)):. sub = s[i:i+10]. if sub in sequence_map:. sequence_map[sub] += 1. else:. sequence_map[sub] = 1...is there a way to do this more blankically?..also how do i do the reverse blankically, as in interating through the dict and composing a list where value is equal to something?..[k for k, v in sequence_map.items()]"
]
result=tf.argmax(lstm_model.predict(sample)).numpy()
result
array([2, 2, 1, 3], dtype=int64)
def pred(result):
for i in result:
if i==0:
print('csharp')
elif i==1:
print('java')
elif i==2:
print('javascript')
elif i==3:
print('python')
pred(result)
javascript
javascript
java
python
Reference
Deep Learning Architectures
for Sequence Processing
Ian Goodfellow, Yoshua Bengio and Aaron Courville (2016). Deep Learning. MIT Press,pp.389-413